In last week’s publication (For a Few Bitcoin More), we presented a Bitcoin cash & carry trade. It’s a live trade, i.e., it’s on my book.
As promised we aim to update our trade ideas regularly and keep you posted with relevant information. This week, we are looking into the sensitivity of the trade to changes in the basis.
Trade recap from 22 June
- Short 2 lots of the July 2020 ICE BAKKT Bitcoin futures contract at $9,482.5
- Long 2 spot BTC on Bitstamp at $9,415.35
This trade implied an annualized funding basis of 11.94%. This basis is the annualized percentage difference between the spot price and the futures price. A market trading in contango, as is the case here, offers incentives for miners and other market participants that are long spot BTC to hedge their exposure and engage in cash & carry trades.
Where are we now?
- Settlement price of the Jul 2020 ICE BAKKT Bitcoin futures contract on Thursday, 2 July: $9,087.5
- Bitstamp BTC spot price on Thursday, 2 July at 5pm ET (settlement time of the futures contract): ~$9,060
Implied annualized funding basis as of Thursday, 2 July: 8.88%
Gross PL = ($9,060 – $9,415.35) * 2 + (9,087.5 – $9,482.5) * -2 = $79.3
What drives the PL?
The futures and the spot price will converge as the futures contract approaches expiration, driving the basis toward zero. Thus, the expected gross PL of the above trade is ($9,482.5 – $9,415.35) * 2 = $134.3.
But how do we get there? Is this a straight line whereby each day we’ll accrue 1/nth of the expected PL, where n is the number of days between trade entry and the expiration date of the futures contract? Quick answer: no, because our PL is not only a function of time (theta); it also depends on how the basis changes over the lifetime of the trade.
The daily theta PL of our trade, initiated on 22 June with a futures expiration on 15 July, is:
$134.3/n = $134.3/23 = $5.83
On July 2, our trade is 10 days “old” and thus our expected PL from theta is $5.83 * 10 = $58.3.
We’ve made more than this though ($79.3) and, as you may have guessed, the extra PL of $20.9 ($10.45 per contract) is due to a reduction in the basis since trade entry.
BV01
You may have heard of DV01, the dollar value of 1 basis point, which measures the price exposure of a bond to a yield change of a single basis point. Let’s adapt this concept to our Bitcoin cash & carry trade and define it as the amount that will be made or lost if the basis changes by 1%.
Futures Price = Spot Price * (1 + Contract Basis)
Contract Basis = Futures Price / Spot Price – 1
Looking at our trade, the Contract Basis is $9,482.5 / $9,415.35 – 1 = 0.71%, which equates to 11.94% annualized based on 23 days to expiration.
Let’s now change the annualized basis to 8.88%, the level observed on 2 July.
Contract Basis = (1 + 8.88%) ^ (13/365) – 1 = 0.3%
13 is the number of days left to contract expiration.
Futures Price = $9,060 * (1 + 0.3%) = $9,087.5, which matches the settlement price observed on 2 July.
Using the above equations we can now change the annualized basis by 1%, up and down, and calculate the impact of such change. As of the date of trade entry, an instantaneous 1% reduction in the annualized basis would have produced a PL of +$5.35, or about 5.6 basis points per contract. As of 2 July, the same impact is about $3 for a 13-day futures contract, i.e., less than the original amount, due to the now reduced time to expiration.
Based on the BV01 methodology we would expect the futures price to decrease from $9,482.5 to $9,465.96 in case of an instantaneous move from 11.94% to 8.88% in the basis. This would result in a PL of $16.55 per contract, which more than our realized extra PL of $10.45 per contract. On the other hand, if the change in basis would have happened on 2 July, our expected extra PL would be $8.98 per contract, which is less than what we’ve got. As you can see, BV01 is non-linear in time. Another factor is convexity: The linear approximation is only valid for small changes in the basis, but needs a correction factor (convexity adjustment) for larger changes.
Time to code
Without diving into the convexity adjustment, we can estimate the evolution of our PL for different paths of the basis by simulation.
In the plot below, I simulated 100 paths from a Vasicek interest rate model, starting with the observed basis of 11.94% on June 22. The simulation takes us over the next 10 days. For the parameters of the Vasicek model I assumed that the long-term mean of the basis is around 5%, the speed of mean reversion 0.2, and a annualized volatility of 2%. Probably these parameters are way off, but it doesn’t matter much for our example. The average over all endpoints of the paths is 9.67%, which is in the neighborhood of our observed 8.88%.
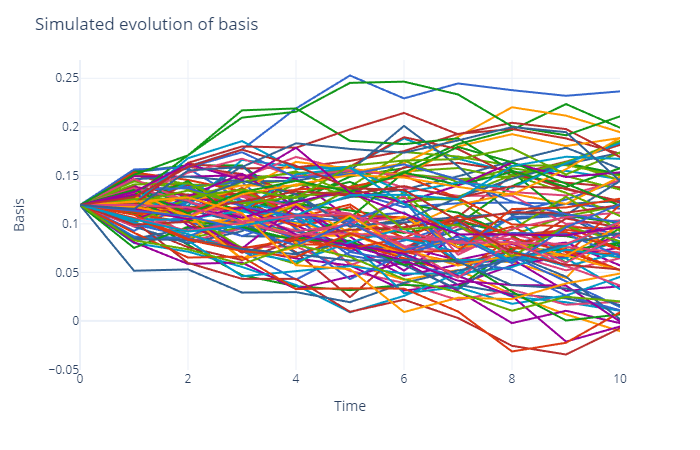
Similar to our example above, for each path and each point in time, we can now calculate the extra PL for each traded contract. Note that we assume in this case that the spot remains constant at $9,415.35, as we only want to illustrate the impact which the dynamics of the basis have on the extra PL. In this instance, the average PL at t=10 (2 July) is $12.96 per contract, with quite a large standard deviation of +/- $31.05. Hence, even with our toy example we can see that there is a considerable variation in the extra PL over time.
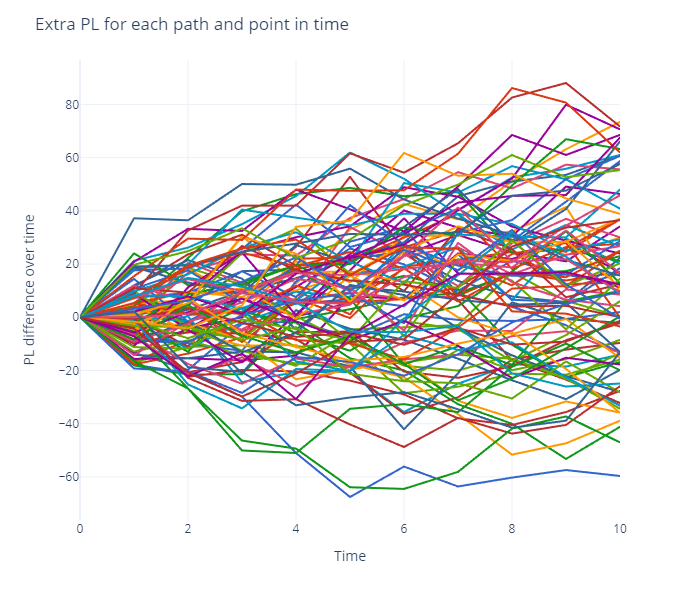
Using these calculations we can explain the intuition behind our observed extra PL of $20.9 ($10.45 per contract) and get a feeling for the trade’s possible PL-volatility (it’s not a straight line if the basis changes). It may also help us determine tactical entry and exit points for the trade.
Note that this is only an idea, not advice of any kind as pointed out in our Disclaimer.

